Einige Beispiele zur Einführung
Welche Szenarien sind nun denkbar, bei denen die Reliabilität, also die Zuverlässigkeit bzw. die Übereinstimmung von zahnmedizinischen oder kieferorthopädischen Messungen eine Rolle spielen? Ein Schwerpunkt liegt in der medizinischen Diagnostik: Stellt ein Zahnarzt bei einem Patienten eine Parodontitis fest und legt sich dazu noch auf einen Schweregrad fest, so sollte ein Kollege, der ihn im Urlaub vertritt, möglichst zum selben Ergebnis kommen – es sei denn, eine spontane Heilung oder Verschlechterung hat inzwischen eingesetzt.
Misst ein Kieferorthopäde wiederholt die Strecke zwischen Nasion und Porion anhand eines Röntgenbildes, so sollten die Abweichungen nur marginal und klinisch irrelevant sein. Neben einzelnen Einschätzungen können auch Mittelwerte verglichen werden, die durch Gruppen zustande gekommen sind, man verspricht sich dadurch eine Erhöhung der Reliabilität. Möglich wäre aber auch die Einschätzung von diversen Klinikern bei der Frage, ob eine Krankheit bei einer Stichprobe von Patienten vorliegt oder nicht. Deutlich wird bereits jetzt, dass die Messung von Reliabilität und Übereinstimmung von einigen Faktoren abhängt, die wir im Folgenden etwas näher beleuchten wollen.
Wer untersucht was?
Im ersten Schritt ist entscheidend, wer oder was die Einschätzungen, Bewertungen oder Messungen vornimmt. Möchten wir untersuchen, wie gut ein und derselbe Zahnarzt eine Einschätzung vornehmen kann, so sprechen wir von Intra-Rater-Reliabilität. Sollen jedoch mehrere Untersucher ein und dasselbe messen, so wird dies als Inter-Rater-Reliabilität bezeichnet. Intuitiv wird man vermuten, dass die Intra-Rater-Reliabilität höher ausfällt als die Inter-Rater-Reliabilität, was meistens auch der empirischen Praxis entspricht. Die nächste Frage beschäftigt sich mit der Zielgröße, also was überhaupt untersucht wird. Hier sind Einschätzungen von Beurteilern möglich (z. B. schwerkrank, krank und gesund), Werte einer kephalometrischen Vermessung (z. B. Winkel zwischen zwei Strecken in Grad) oder die Übereinstimmung bezüglich der Rekonvaleszenz nach einem oralchirurgischen Eingriff zwischen zwei Praxen.
Aus statistischer Sicht interessiert hier vor allem das Skalenniveau der untersuchten Zielgröße, da sich infolge dessen auch die Wahl der statistischen Methode ableitet. Im einfachsten Fall haben wir es mit einem nominalen Merkmal zu tun, das sich nur durch zwei Ausprägungen konstituiert, wie z. B. behandlungsbedürftig oder nicht behandlungsbedürftig. Ein Assistenzarzt und sein Oberarzt mögen diese Einstufung bei 10 Patienten vornehmen, tabellarisch könnte das dann so aussehen:
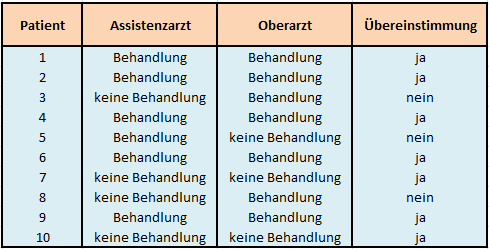
Tabelle 1: Datenmatrix der Einschätzungen zweier Beurteiler
In diesem Beispiel würden sich bei 10 Patienten 7 Übereinstimmungen finden, bei 3 Patienten sind die Untersucher hingegen uneins. Generell kann man dieses Szenario erweitern: Zum einen könnten mehr als zwei Ärzte die Patienten einschätzen, andererseits ist es möglich, dass die Zielgröße aus mehr als zwei Ausprägungen besteht. Hier wäre übrigens Cohen’s Kappa das Mittel der Wahl.
Im nächsten Fall handelt es sich bei der Zielgröße um eine ordinale Variable, weswegen eine Rangbildung möglich ist. Dieses Skalenniveau kommt in den medizinischen Disziplinen häufig vor, da viele Krankheiten nach Schweregraden klassifiziert werden, wie beispielsweise Parodontopathien. Diese werden konventionell in 5 Schweregrade (Grad 0 bis Grad 4) eingeteilt. Nehmen wir hier an, dass 3 Promotionsstudenten insgesamt 10 Patienten diesbezüglich untersuchen und beurteilen müssten, so wird sofort klar, dass die Rangordnung der Schweregrade mitberücksichtigt werden sollte. Wenn Student A und B einen Patienten beurteilen müssen und sich deren Einschätzung nur um eine Stufe der Skala unterscheidet (A: Grad 2, B: Grad: 3), so ist dieser Unterschied weniger gravierend, als wenn sie sich sehr deutlich um 3 Stufen unterscheiden (A: Grad 1, B: Grad 4). Auch für dieses Skalenniveau stehen verschiedene statistische Techniken zur Auswahl, die bekannteste ist Weighted Kappa.
Komplettiert werden unsere Beispiele durch den dritten Fall, bei dem die Zielgröße Kardinalskalenniveau aufweist – man spricht auch von metrischen Variablen. Im Gegensatz zum ordinalen Niveau sind hier auch die Abstände zwischen den Ausprägungen gleich (äquidistant), manchmal liegt darüber hinaus noch ein Nullpunkt vor. Beispiele dafür sind Strecken (gemessen in Millimetern) bei kephalometrischen Studien oder aber die Strahlenbelastung (gemessen in Mikrosievert) in der Radiologie. Auf dieses Skalenniveau werden wir uns im Folgenden konzentrieren.
Welche Arten von Reliabilität gibt es?
Wie eingangs angedeutet, unterscheiden wir in erster Linie die Intra- von der Inter-Rater-Reliabilität. Nicht unerwähnt bleiben sollte in diesem Zuge auch die sogenannte Test-Retest-Reliabilität, wobei der Fokus auf der Methode liegt. Zur Unterscheidung der Konzepte soll die folgende Darstellung dienen, gemessen wurde der Winkel der Bisslage in vertikaler Ebene mittels FRS, das 3 Tage später nochmals erstellt wurde, die relevanten Messreihen sind orange hinterlegt:
Intra-Rater:

Inter-Rater:

Test-Retest:

Tabelle 2: Datenmatrix einer quantitativen Zielgröße mit wiederholten Messungen
Grundlage für die Intra- und Inter-Rater-Reliabilität ist ein und dieselbe Röntgenaufnahme der Patienten, für die Test-Retest-Methode wurde 3 Tage später nochmals eine zweite Aufnahme erstellt. Wir wollen uns im Folgenden mit der Intra- und Inter-Rater-Reliabilität beschäftigen.
Ein einfaches statistisches Modell
Nach Erhebung der Daten stellt sich nun die Frage, wie groß die Differenzen zwischen den Messreihen ausfallen und wie diese überhaupt zustande gekommen sind. Hier hilft uns die klassische Testtheorie, die besagt, dass sich ein Messwert aus einem wahren Wert und einem Fehleranteil zusammensetzt. Ohne unsere mathematischen Fähigkeiten zu sehr zu strapazieren, können wir mit einfacher Algebra die folgende Gleichung ohne weiteres nachvollziehen:
Messwert = Wahrer Wert + Fehler
In diesem Zusammenhang ist wichtig zu unterscheiden, ob wir den wahren Wert überhaupt kennen oder nicht. Existiert ein Goldstandard oder ein Verfahren, von dem wir wissen, dass es reliabel ist, so kennen wir den wahren Wert und vergleichen ihn mit unserem Messwert. Ist der wahre Wert jedoch nur ein hypothetisches Konstrukt, so wird er bei metrischem Skalenniveau meist als Mittelwert mehrerer Messungen definiert. Es fällt auf, dass die erste Variante methodisch leichter zu handhaben ist. Nehmen wir beispielsweise an, wir kennen den exakten Winkel zwischen Frankfurter Horizontale und der Sella-Nasion-Linie bei einem ausgewählten Patienten, so entspräche dies dem wahren Wert und jede Abweichung davon demzufolge dem Fehler. Das Ziel ist es folglich, diesen Fehler möglichst gering zu halten.
Unter der Lupe: Der Fehleranteil
Betrachten wir jede Abweichung vom wahren Wert als Fehler, so hilft es im nächsten Schritt, den Fehleranteil noch weiter zu zerlegen. Unsystematische Schwankungen bei Bewertungen oder Messungen sind völlig normal, wir bezeichnen diesen Fehleranteil auch als zufälligen Fehler. Dem entgegen steht der systematische Fehler, welcher durch eine Verzerrung (Bias) hervorgerufen wird. Ein Bias kennen die meisten wohl noch aus ihrer Schulzeit: Manche Lehrer sind strenger und benoten die Schüler schlechter als andere Lehrer. Da sich diese Strenge nicht nur bei einem Schüler, sondern bei allen zeigt, ist diese Tendenz systematisch. Übertragen auf die Kephalometrie könnte dies bedeuten, dass ein Untersucher immer etwas zu hoch oder zu niedrig ansetzt – und zwar bei allen Messungen bzw. allen Patienten. Auch eine Waage, die stets 2 kg zu viel anzeigt, hat einen systematischen Fehler. Analog zur ersten Gleichung können wir eine zweite formulieren, auf die wir später noch einmal zurückkommen werden:
Gesamter Fehler = Zufälliger Fehler + Systematischer Fehler
Eine recht bekannte Darstellung mithilfe von Zielscheiben illustriert das Konzept, wobei man bei hoher Reliabilität auch synonym von hoher Genauigkeit spricht, welche wiederum hohe Präzision und hohe Richtigkeit voraussetzt:
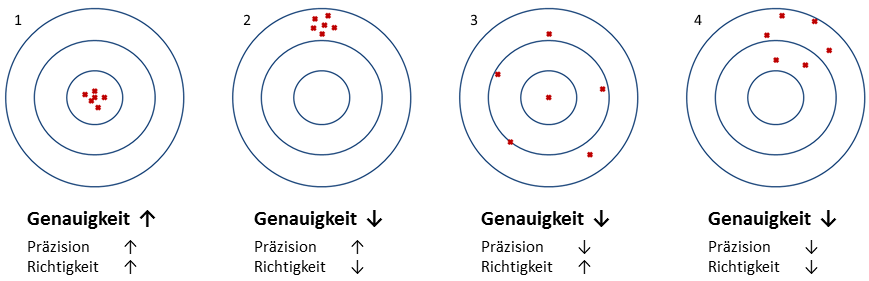
Abbildung 1: Illustration der Konzepte Präzision und Richtigkeit anhand einer Zielscheibe
Nur im ersten Fall kann man offensichtlich von einer hohen Reliabilität ausgehen, während im zweiten Fall die Messungen kaum schwanken, aber dafür weit weg vom Mittelpunkt liegen. Dieser Fall entspricht somit einem geringen zufälligen Fehler (hohe Präzision), aber hohen systematischen Fehler (geringe Richtigkeit), da alle Messungen in eine bestimmte Richtung verzerrt sind – ein Bias liegt vor. Im dritten Fall scheint der zufällige Fehler groß zu sein (geringe Präzision), wobei hingegen die Richtigkeit hoch ist (berechnete man den Mittelwert aller Messungen, würde man im Zentrum liegen). Fall 4 hingegen entspricht dem Worst Case: Weder Präzision noch Richtigkeit sind gegeben und daher natürlich auch keine Genauigkeit.
Wir können festhalten, dass die Präzision mit dem zufälligen Fehler und der Streuung assoziiert ist, während die Richtigkeit mit dem systematischen Fehler und dem Abstand zum wahren Wert charakterisiert wird. Um hohe Reliabilität zu erreichen, muss Genauigkeit gegeben sein, deren notwendige Bedingungen Präzision und Richtigkeit sind. An dieser Stelle sei angemerkt, dass diese Konzepte auch im Qualitätsmanagement oder in Produktionsprozessen Anwendung finden, wenn es darum geht, Abweichungen oder Variabilität zu quantifizieren.
Warum der Korrelationskoeffizient keine gute Idee ist
Fall 2 der letzten Grafik entspricht einem ausgeprägten Bias und nur wenig Streuung der Messwerte, der zufällige Fehler ist also gering und der systematische hoch. Jemand mit Kenntnissen der deskriptiv-explorativen Statistik könnte nun auf die recht naheliegende Idee kommen, einfach die Korrelation zweier Messreihen zu berechnen und dies als Maß für die Reliabilität zu verwenden. Allerdings wird dabei übersehen, dass der Korrelationskoeffizient – hier die Pearson-Korrelation – nur den linearen Trend zweier Messreihen quantifizieren kann, nicht jedoch die absolute Übereinstimmung:
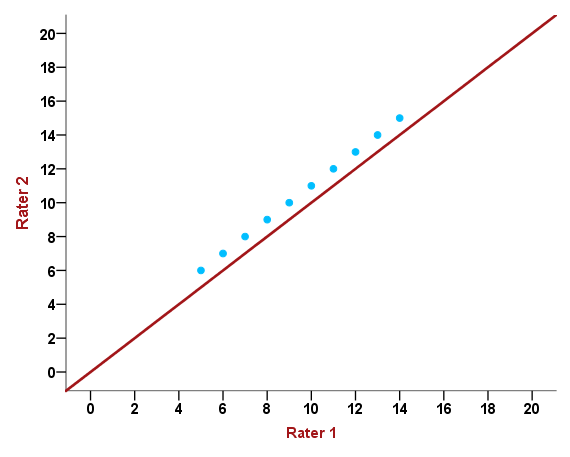
Abbildung 2: Scatterplot der Einschätzungen zweier Beurteiler
Anhand dieser Grafik ist zu erkennen, dass Rater 2 bei seinen Messungen jeweils um eine Einheit höher liegt als Rater 1 (6 vs. 5, 12 vs. 11, 9 vs. 8 usw.), wobei die 10 Messungen durch die blauen Punkte dargestellt werden. Würden wir den Korrelationskoeffizienten r berechnen, so würde dieser genau 1 betragen, da alle Punkte auf einer gedanklichen Linie liegen. Für eine perfekte Übereinstimmung müssten aber alle Messungen der beiden Rater auf der Winkelhalbierenden (rote Linie) liegen. Der Bias, der durch Rater 2 (oder aber Rater 1) verursacht wird, hat keine Auswirkungen auf den Korrelationskoeffizienten – der systematische Fehler wird nicht „bestraft“. Zusammenhangsmaße sind aus diesem Grund für Reliabilitätsstudien nicht geeignet.
Die Intra-Klassen-Korrelation
Kommen wir zurück auf unsere ursprüngliche Gleichung lautete diese:
Messwert = Wahrer Wert + Fehler
oder etwas mathematischer:
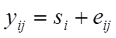
wobei s für „subject“ und e für „error“ steht.
Wir verwenden hier die englischen Abkürzungen, da diese deutlich geläufiger sind. Danach setzt sich der Messwert yij des i-ten Subjekts (z.B. Patient, Röntgenbild, klinischer Parameter) und des j-ten Raters zusammen aus dem wahren Wert si des Subjektes i und einem Fehleranteil eij. In diesem einfachen Modell unterscheiden wir also nicht zwischen zufälligem und systematischem Fehler. Wir könnten dies auch gar nicht, da wir hier davon ausgehen, dass die Subjekte jeweils von unterschiedlichen Ratern begutachtet worden sind und somit der Bias eines Raters nicht zu erfassen ist.
Im nächsten Schritt geht es nun darum, die Varianzen der drei Komponenten zu schätzen. Es gilt, dass die gesamte Varianz sich aus der Varianz der wahren Werte und der Varianz der Fehler zusammensetzt (auf die mathematische Herleitung wollen wir hier verzichten):
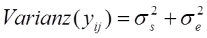
Der griechische Buchstabe Sigma (σ) steht dabei für die Standardabweichungen in der Population, quadrieren wir diese, erhalten wir die Populationsvarianzen.
Setzen wir nun die Varianz der wahren Werte (σs2) ins Verhältnis zur gesamten Varianz, erhalten wir die sogenannte Intra-Klassen-Korrelation (engl. Intraclass Correlation Coefficient, ICC):
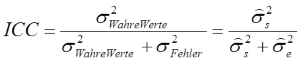
Das Dach über dem Sigma steht dafür, dass es sich um geschätzte Populationsvarianzen handelt, da wir diese aus unserer Stichprobe ableiten müssen. Aus der Formel wird ersichtlich, dass der ICC dann gegen sein mögliches Maximum von 1 strebt, je kleiner die Fehlervarianz ist. Im Idealfall gibt es überhaupt keine Messfehler und somit keine Variabilität – die Fehlervarianz beträgt 0. Wir erhalten dann einen ICC von 1. Mit steigender Fehlervarianz sinkt hingegen der ICC, generell liegt der Wertebereich zwischen 0 und 1.
Betrachten wir zur Veranschaulichung ein kurzes Beispiel, bei dem verschiedene Landmarks in einem 3D-Röntgenbild vermessen wurden. Wir gehen dabei davon aus, dass die einzelnen Messungen durch verschiedene Untersucher zustande kamen und nicht nur durch 2 Untersucher – wie es die Tabelle suggerieren könnte.
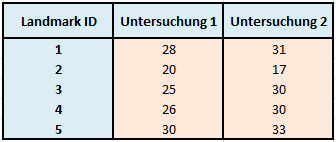
Tabelle 3: Datenmatrix von Strecken in mm mehrerer Untersucher
Der ICC wird nun mithilfe einer einfaktoriellen ANOVA mit zufälligen Effekten berechnet. Die klassische ANOVA-Tabelle liefert dabei die nötigen mittleren Quadratsummen (Mean Squares), aus denen die Varianzkomponenten berechnet werden können (vgl. dafür die Formeln von Shrout & Fleiss, 1979). Es ergeben sich die folgenden Werte:
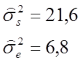
Auf den ersten Blick ist zu erkennen, dass die geschätzte Varianz der wahren Werte etwa 3x höher ausfällt als die des Fehlers. Der ICC beträgt demnach:
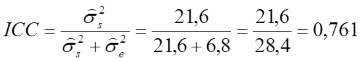
Wir können nun schlussfolgern, dass gut drei Viertel der gesamten Varianz (76,1%) auf die wahren Werte entfallen und etwa 23,9% durch Fehlerquellen generiert wurden. In Anlehnung an Fleiss (1986) können die Werte des ICC folgendermaßen interpretiert werden:
0,00 – 0,40 poor
0,40 – 0,75 fair to good
0,75 – 1,00 excellent
Diese Einteilung erscheint etwas grob und Fleiss wusste wohl schon, dass hier eine Vergleichbarkeit suggeriert wird, die methodisch einige Schwierigkeiten aufwirft und streng genommen nur eingeschränkt zulässig ist. Dennoch wird dieser Vergleich zwischen ICCs aus unterschiedlichen Studien mit verschiedenen Populationen immer wieder vollzogen und findet sich häufig bei Reliabilitätsstudien aus dem Bereich der Zahn- und Humanmedizin. Warum es immer wieder zu diesem methodischen Fehler kommt, ist durchaus nachvollziehbar und wir wollen uns daher dieser Problematik im Speziellen widmen.
Kritik am ICC: Die Varianz zwischen den Subjekten ist entscheidend
Lassen Sie uns nochmals unser Beispiel zu den Landmarks aufgreifen und die Daten ein wenig manipulieren, um die Auswirkungen auf den ICC untersuchen zu können. Die folgende Tabelle zeigt links die ursprünglichen Werte und rechts neue Werte:
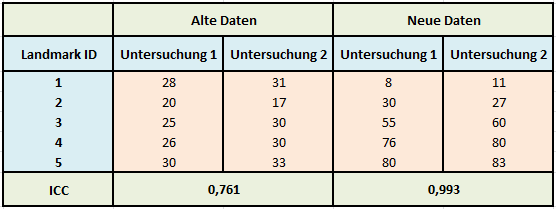
Tabelle 4: Vergleich des ICC zwischen zwei unterschiedlichen Datensätzen
Betrachten wir nur Untersuchung 1 der alten und neuen Daten, so fällt auf, dass die neuen Daten deutlich mehr streuen, also eine größere Varianz aufweisen. Gemessen wurden hier Strecken in mm zwischen verschiedenen Landmarks und einem Referenzpunkt. Somit verursacht nur die Lage der Landmarks (sind sie weit weg vom Referenzpunkt, sind die Strecken größer) die Varianz in den Daten, obwohl dies für die Einschätzung der Reliabilität völlig unerheblich ist. Vergleichen wir die Abweichungen zwischen Untersuchung 1 und 2 für die alten und die neuen Daten, so sind diese identisch: Für Landmark 3 z. B. beträgt die Differenz zwischen der ersten und der zweiten Untersuchung jeweils -5 mm (25-30 bzw. 55-60), sie sind also gleich.
Wenn die Lage der Landmarks allerdings gar keine Rolle für die Zuverlässigkeit wiederholter Untersuchungen spielt, sollte der ICC gleichwohl konstant bleiben. Vergleichen wir beide ICCs, so hat sich dieser zu den neuen Daten stark erhöht und es ist eine nahezu perfekte Reliabilität zu beobachten (ICC=0,993), die nur durch die Erhöhung der Varianz der Werte in der Stichprobe verursacht wurde, die Abweichungen blieben dieselben. Streng genommen darf der ICC also zwischen Untersuchungen nur verglichen werden, wenn σs2 konstant ist – was praktisch niemals der Fall ist, sondern nur bei ein und derselben Untersuchung, bei der sich der Pool an Subjekten nicht verändert.
Auch kann uns der ICC nicht die Einschätzung abnehmen, ob Abweichungen klinisch relevant sind oder nicht. Im neuen Datensatz möge die maximale Abweichung von -5 mm bereits zu viel sein und aus praktischen Gründen keineswegs mehr tolerierbar, ein ICC von 0,993 ließe sich inhaltlich damit kaum vereinbaren. Dieses Phänomen lässt sich recht häufig in medizinischen Fachartikeln und Dissertationen finden: Die Vermischung der Konzepte statistischer Signifikanz oder eines Kennwertes und die klinische Relevanz. Beide sind bei der Interpretation von Studienergebnissen unbedingt zu trennen und nicht zu vermischen.
Die Berücksichtigung der Fehlerkomponenten
In unserem ersten Modell zum ICC haben wir den Fehleranteil nicht in seine Komponenten zerlegt, da wir davon ausgegangen sind, dass die Messungen von verschiedenen Ratern über die Landmarks erfolgten und ein systematischer Einfluss eines Raters somit nicht messbar wäre. Wollen wir nun die Intra-Rater-Reliabilität berechnen, so wird jedes Subjekt von einem Rater mehrfach gemessen oder eingeschätzt. Analog dazu können wir die Inter-Rater-Reliabilität berechnen, wenn die gleichen Rater alle Subjekte einschätzen und die Rater von Subjekt zu Subjekt nicht variieren. Bleiben wir konsequenterweise bei unserem Beispiel zur Vermessung der Landmarks mit den gleichen Werten, würde unsere Datenmatrix die folgende Gestalt annehmen:
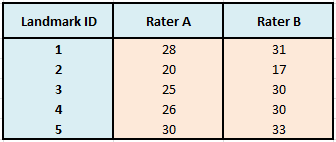
Tabelle 5: Datenmatrix von Strecken in mm zweier Untersucher
Rater A würde alle 5 Landmarks vermessen und genauso Rater B. Gehen wir davon aus, dass die Rater eine (theoretische) Zufallsauswahl aus einem Pool an Ratern darstellen, so können wir die Inter-Rater-Reliabilität mit einer zweifaktoriellen Varianzanalyse herleiten, wobei Subjekte und Rater als zufällige Effekte zu behandeln sind. Wir sind nun in der Lage, zufällige und systematische Einflüsse zu trennen, da uns ein vollständiges faktorielles Design vorliegt (Landmark x Rater). Unsere ursprünglichen Gleichungen lauteten:
Messwert = Wahrer Wert + Fehler
Gesamter Fehler = Zufälliger Fehler + Systematischer Fehler
Setzen wir nun die zweite Gleichung in die erste ein, so ergibt sich:
Messwert = Wahrer Wert + Systematischer Fehler + Zufälliger Fehler, oder:
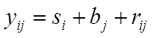
Anstatt des ursprünglichen Fehlerterms eij modellieren wir nun bj (Bias des j-ten Raters oder systematischer Fehler) und rij (Residuum des i-ten Subjektes des j-ten Raters bzw. zufälliger Fehler). Eine erste Betrachtung unseres zugegeben sehr kleinen Datensatzes lässt erkennen, dass Rater B bei den Streckenmessungen generell etwas großzügiger zu sein scheint als Rater A – liegt er doch bei allen Landmarks mit Ausnahme von Landmark 2 über denen seines geschätzten Kollegen. Es könnte also ein Bias vorliegen, den wir nun in unserem Modell explizit berücksichtigen. Auch hier addieren sich die Varianzanteile wieder zur Gesamtvarianz:
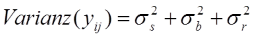
Für den ICC ergibt sich dann:
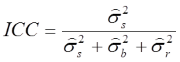
Nach der Einteilung von Shrout & Fleiss (1979) liegt hier der ICC(2) vor, während es sich beim ersten Modell um den ICC(1) handelte. Da wir auch hier die Populationsvarianzen nicht kennen, müssen wir diese anhand unserer Stichprobenvarianzen schätzen. Wir erhalten danach:
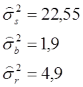
Der zufällige Fehler hat eine deutlich größere Varianz (4,9) als der systematische (1,9). Addiert man die Varianzen beider Fehleranteile, ergibt sich wieder der ursprüngliche Wert von 6,8 und entspricht exakt der Varianzschätzung aus dem ersten Modell. Die Varianz für die Subjekte (hier Landmarks) vergrößert sich etwas (22,55), da zur Berechnung dieser Varianzkomponente nicht mehr der gesamte Fehler, sondern nur noch der zufällige Fehler berücksichtigt wird. Wir berechnen:
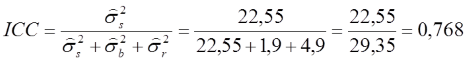
Wir sehen, dass sich der ICC nur marginal zum ersten Modell ändert (0,768 vs. 0,761), was vor allem daran liegt, dass der Bias nur eine geringe Varianz verursacht.
Shrout & Fleiss schlugen in ihrer Publikation noch ein weiteres Modell vor, das die Rater als festen Effekt behandelt. Es ergibt sich dann ein zweifaktorielles gemischtes Modell, das jedoch in der Praxis nur selten zum Einsatz kommt, da es keine Generalisierung der Ergebnisse auf alle Rater zulässt. Sie bezeichneten dieses Modell als ICC(3).
Abschließend sollte erwähnt werden, dass es möglich ist, den ICC nicht nur für Einzelwerte wie in unserem Beispiel zu berechnen, sondern auch für Durchschnittswerte. Eine weitere Möglichkeit besteht bei den Zwei-Wege-Modellen ICC(2) und ICC(3) darin, Konsistenz oder absolute Übereinstimmung zu wählen. Entscheiden wir uns für Konsistenz, so wird der systematische Fehler nicht berücksichtigt (vgl. dazu auch das Beispiel zur Eignung des Korrelationskoeffizienten), während bei der absoluten Übereinstimmung jegliche Abweichung in die Berechnung eingeht. Ist man im Zweifel, welches Modell zu wählen ist, sollte man sich für das strengere entscheiden.
Die Bland-Altman-Methode
Nachdem klar geworden ist, dass es sich bei der Intra-Klassen-Korrelation zwar um ein durchaus populäres und häufig verwendetes Analyseinstrument im Rahmen von Reliabilitätsstudien handelt, wissen wir, dass damit auch einige Schwächen und Einschränkungen verbunden sind, die uns das Leben im Hinblick auf Vergleichbarkeit und Robustheit schwer machen. Auch die Interpretation des ICC scheint nicht ungefährlich zu sein – im Besonderen, wenn man sich der statistischen Eigenschaften nicht vollumfänglich bewusst ist und den ICC nur als Kennwert sieht, der Werte von 0 bis 1 annehmen kann.
Unter anderem aus diesen Gründen waren Bland und Altman (1986) motiviert, ein Verfahren zu entwickeln, dass sich der Untersuchung von Reliabilität und Übereinstimmung gerade bei medizinischen Fragestellungen anders nähert und die Schwächen konventioneller Methoden überwinden sollte.
Beginnen wir wieder mit dem Fall, bei dem zwei zufällig ausgewählte Rater alle Subjekte vermessen und die Ergebnisse anschließend in einer Datenmatrix aufbereitet wurden. Zusätzlich wurden jeweils noch die Differenzen sowie die Mittelwerte berechnet, insgesamt lagen 200 vollständige Messungen pro Rater vor. Hier ein Auszug des Datensatzes, bei dem die ersten fünf und die letzten drei Fälle aufgeführt sind:
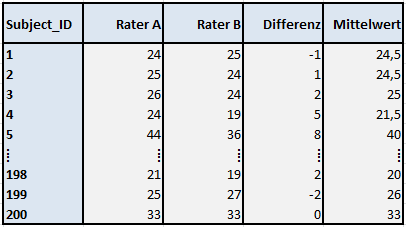
Tabelle 6: Datenmatrix als Grundlage zur Erstellung eines Bland-Altman-Plots
Läge eine perfekte Übereinstimmung der Rater A und B vor (hier sind es wiederum Messungen in mm), so müssten die Differenzen 0 betragen und die Mittelwerte müssten mit den Werten der Rater übereinstimmen. Greifen wir nun wieder unser ursprüngliches Konzept auf, bei dem wir zwischen zufälligem und systematischem Fehler unterschieden haben. Besteht kein systematischer Fehler bzw. Bias eines Raters, so müsste der Mittelwert aller Differenzen ebenfalls 0 ergeben, da sich die zufälligen Fehler ausgleichen. Ist im Mittel über alle 200 Subjekte die Differenz Rater A – Rater B positiv, also >0, so würde das bedeuten, dass die Messungen von Rater A größer ausfallen, als die von Rater B – ein Bias läge vor. Sind die Differenzen im Mittel im negativen Bereich, also <0, so träfe der umgekehrte Fall zu.
Der zufällige Fehler hingegen wird durch die Streuung (=Standardabweichung, SD) der Differenzen beschrieben, die der Wurzel aus der Varianz entspricht. Gehen wir weiter davon aus, dass die Differenzen annähernd normalverteilt sind, so können wir Grenzen festlegen, in denen ca. 95% aller Differenzen liegen. Diese Grenzen wurden von Bland & Altman auch als Limits of Agreement bezeichnet. Wir machen uns somit die Eigenschaften der Normalverteilung zunutze. Kennen wir diese Limits of Agreement (LoA), muss im letzten Schritt beurteilt werden, ob diese klinisch relevant sind oder nicht. Es kann dann eine abschließende Beurteilung der Reliabilität vorgenommen werden.
Entscheidend ist, dass bei dieser Methode die Streuung bzw. Varianz der Rohwerte keine Rolle mehr spielt, sondern ausschließlich der Differenzen und deren Verteilung ausschlaggebend sind, was ein deutlicher Vorteil gegenüber dem ICC ist. Im Folgenden ist der Bland-Altman-Plot – generiert aus den Daten unseres Beispiels – dargestellt:
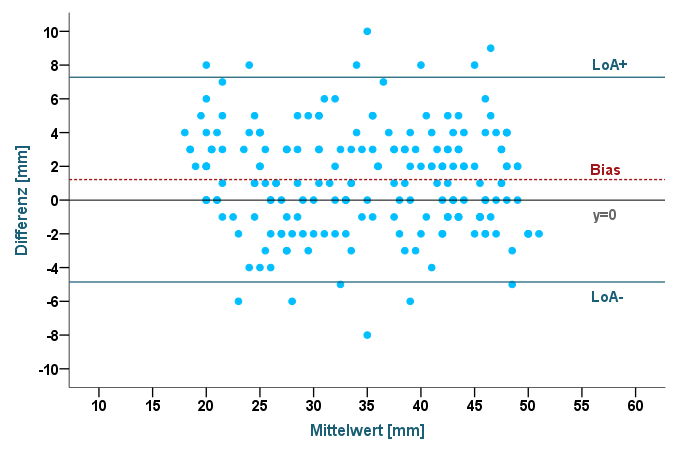
Abbildung 3: Bland-Altman-Plot
Die blauen Punkte spiegeln die Differenzen wider (y-Achse), die gegen die Mittelwerte (x-Achse) der Messungen von Rater A und B abgetragen wurden. Maß Rater A beispielsweise 35 mm und Rater B 38 mm, so würde die Differenz 35-38=-3 mm betragen, der Mittelwert entspräche (35+38)/2=36,5 mm.
Berechnen wir nun den Mittelwert der 200 Differenzen, so erhalten wir den Wert 1,22 – er entspricht der rot gestrichelten Linie im Diagramm und manifestiert den Bias: Rater A misst im Mittel 1,22 mm mehr als Rater B. Um diesen Unterschied auch grafisch deutlich zu machen, wurde zusätzlich die Linie y=0 eingezeichnet. Gäbe es keinen Bias, so würden die Linien sich überlappen. Wollen wir prüfen, ob der Bias statistisch signifikant ist, so können wir ihn mittels T-Test gegen 0 testen. Da die Differenzen entscheidend sind, wollen wir uns deren Verteilung nochmals in einem Histogramm vergegenwärtigen:
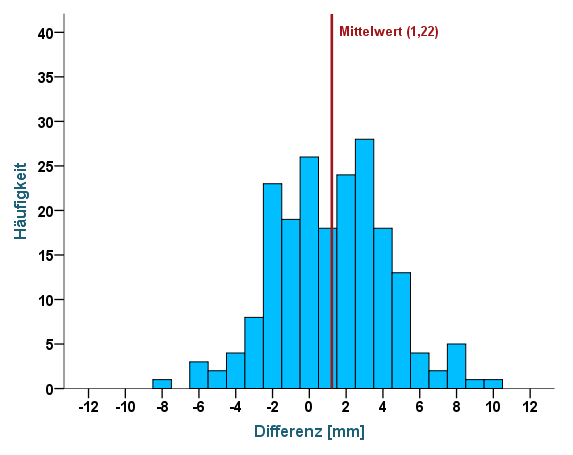
Abbildung 4: Histogramm der Differenzen
Wir können erkennen, dass die Differenzen sich annähernd normal um ihren Mittelwert von 1,22 mm (nicht 0!) verteilen. Im nächsten Schritt berechnen wir nun die Standardabweichung (SD) der Differenzen zur Quantifizierung des zufälligen Fehlers, die im vorliegenden Beispiel 3,09 beträgt. Greifen wir auf die Eigenschaften der Normalverteilung zurück, so wissen wir, dass ca. 95% der Werte im Bereich von -1,96 bis +1,96 Standardabweichungen liegen. Genau diese Grenzen entsprechen den Limits of Agreement, die wir nun ohne große Mühe berechnen können:
LoA = MDiff ± (1,96 x SDDiff)
Die obere Grenze (LoA+) ergibt sich somit zu: 1,22 + (1,96 x 3,09) = 1,22 + 6,06 = 7,28
Die untere Grenze (LoA-) entsprechend zu: 1,22 – (1,96 x 3,09) = 1,22 – 6,06 = -4,84
Wir können festhalten, dass ca. 95% der Abweichungen zwischen den Ratern im Bereich von -4,84 mm bis 7,28 mm liegen. Hätten wir einen klinischen Toleranzbereich von ±10 mm, so könnten wir also von ausreichender Inter-Rater-Reliabilität sprechen. Läge der Toleranzbereich bei nur ±5 mm, so wäre die Reliabilität nicht mehr gegeben, da die obere Grenze durchbrochen wäre. Für die Limits of Agreement als auch für den Bias können auch die entsprechenden Konfidenzintervalle berechnet werden. Besteht zwischen den Differenzen und den Mittelwerten eine Abhängigkeit – wird zum Beispiel die Varianz der Differenzen mit wachsendem Mittelwert größer – so kann dies häufig mit Transformationen (z.B. dem natürlichen Logarithmus) gelöst werden.
Abschließend sei erwähnt, dass bei Untersuchungen zur Reliabilität und Übereinstimmung bei metrischem Skalenniveau nicht nur der Mittelwert der Differenzen, sondern deren Verteilung von zentraler Bedeutung ist. Die Varianz der Rohdaten hingegen hat keinen Einfluss auf die Ergebnisse. Die Bland-Altman-Methode besticht durch ihre Vorzüge, wie die recht einfache Berechnung der nötigen statistischen Kennwerte und einer intuitiven und übersichtlichen Darstellung. Vergleiche zwischen Studien sind nun möglich. Das Verfahren hat sich inzwischen zum Goldstandard etabliert und findet mehr und mehr Einzug in statistische Softwarepakete. Darüber hinaus sind auch weitere Publikationen der Autoren äußerst lesenswert und gehören zu den populärsten Schriften in der medizinischen Statistik.
Quellen:
Shrout, P.E., Fleiss, J.L. (1979). Intraclass correlation: Uses in assessing rater reliability. Psychological Bulletin. 1979;86, S.420-428.
Fleiss, J.L. (1986). The Design and Analysis of Clinical Experiments. New York: John Wiley & Sons.
Bland, J.M., Altman, D.G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986 Feb 8, S.307-310.
