Eine Viertelstunde später sitzen Sie in Ihrer Kneipe an der Bar und fachsimpeln mit dem etwas in die Jahre gekommenen Wirt über die neuesten politischen Entwicklungen. In jenem Moment betritt ein etwas zwielichtig anmutender Mann die Kneipe und setzt sich neben Sie an die Bar. Obwohl Sie ihn vorher noch nie gesehen haben, entwickelt sich nach ein paar Minuten des zurückhaltenden Schweigens ein kleines Gespräch, in dem Sie sich nach einer Weile unter anderem auch als Hobbyspieler zu erkennen geben, der auch einer kleinen Sportwette hier und da nicht abgeneigt ist. „Sie spielen also gern, wie?“, fragt Sie der etwas undurchsichtige Gegenüber, der Sie soeben auf eine weitere Runde eingeladen hat. Im Inneren wanken Sie zwischen Sympathie und vorsichtiger Distanz zu Ihrem neuen Bekannten, als Sie seine Frage mit einem Kopfnicken bejahen. „Nun, dann habe ich was für Sie, es dürfte Sie interessieren.“
Nach einer kurzen Pause antworten Sie: „Worum geht es?“, und drehen sich nun vollends Ihrem Thekennachbarn zu. „Ein Spiel, das Sie kaum ablehnen können“, so der Undurchsichtige weiter, „und das außerdem leicht zu verstehen ist. Wir brauchen dazu lediglich eine Münze. Jeder von uns bestimmt eine konkrete Kombination von 3 Münzwürfen, dann werfen wir die Münze so lange, bis entweder Ihre Kombination oder meine das erste Mal auftritt. Wenn Ihre Kombination als erstes geworfen wird, ist das Spiel vorbei und Sie gewinnen den Einsatz, trifft jedoch meine zuerst ein, gewinne ich und das Spiel ist beendet.“ „Ich verstehe“, entgegnen Sie ihm aufmerksam folgend, „wenn ich beispielsweise sage, Zahl-Zahl-Zahl und Sie setzen auf Kopf-Kopf-Kopf, dann gewinne ich, sobald 3 x Zahl hintereinander fällt und Sie, wenn 3 x hintereinander Kopf geworfen wird, richtig?“
„So ist es“, bemerkt Ihr Gegenüber zustimmend, „natürlich ist auch eine Kombination wie Kopf-Zahl-Kopf möglich, ganz nach Ihrem Belieben.“ „In Ordnung“, entgegnen Sie, „aber wo liegt der Reiz Ihres Spiels, wir könnten genauso gut einmal werfen und nur das Glück entscheidet, wer am Ende gewinnt und wer verliert.“ „Nicht ganz“, entgegnet der Undurchsichtige, „ich gewähre Ihnen noch zwei weitere Vorteile: Wenn ich gewinne, bekomme ich 10 Euro von Ihnen, wenn Sie gewinnen, dann bekommen Sie 15 Euro von mir! Darüber hinaus dürfen Sie immer als Erster Ihre Kombination wählen, ich muss dann zwingend eine andere aussuchen. Und um jeden Zweifel auszuräumen, lieber Freund, benutzen wir eine Ihrer Münzen und nur Sie dürfen die Münze werfen. Nun, was sagen Sie?“ Verblüfft hören Sie dem Undurchsichtigen zu und fangen an, tiefer über die Sache nachzudenken. Entweder ist der Mann ein Tölpel oder aber ein raffinierter Betrüger, resümieren Sie nachdenklich. „Einen Moment, lassen Sie mich kurz überlegen“, erwidern Sie dem Undurchsichtigen. Dass der Abend noch solch eine Wendung nehmen sollte, hatten Sie nicht erwartet. Da Zahlen allerdings schon immer Ihre Leidenschaft waren, gehen Sie das ominöse Spiel analytisch an:
Bei 3 Münzwürfen ergeben sich insgesamt 2³ = 8 verschiedene Kombinationen:
K-K-K K-K-Z K-Z-K K-Z-Z
Z-Z-Z Z-Z-K Z-K-Z Z-K-K
Die Chance für Kopf oder Zahl ist bei einer fairen Münze gleichwahrscheinlich, beträgt also jeweils 50%. So weit, so gut. Da jeder einzelne der drei Würfe unabhängig ist – man nennt dies auch disjunkte Ereignisse oder stochastische Unabhängigkeit – ist jede der 8 Möglichkeiten gleichwahrscheinlich und beträgt damit pro Kombination 1/8. Keine Kombination aus 3 Münzwürfen ist somit einer anderen überlegen, es gibt keine guten und keine schlechten, alle sind gleich „gut“ oder „schlecht“. Die Chance, zu gewinnen, ist damit ebenso hoch, wie die Chance, zu verlieren, sie beträgt jeweils 50%. Im nächsten Schritt berechnen Sie sogleich den Erwartungswert des Spiels, der, wie Sie noch wissen, den Ausgang des Spieles, also Gewinn oder Verlust in Euro, mit den jeweiligen Wahrscheinlichkeiten multipliziert. Rasch berechnen Sie, dass der Erwartungswert (E)
E = 1/2 x (-10 €) + 1/2 x (+15 €) = 2,50 €
beträgt, somit positiv ist und Sie im Mittel 2,50 Euro pro Durchgang gewinnen. Sie können es kaum abwarten, die Herausforderung des Undurchsichtigen anzunehmen. „Lassen Sie uns anfangen“, eröffnen Sie die erste Runde siegesgewiss und kramen eine Münze aus Ihrer Hosentasche hervor.
Etwa eine Stunde später, Sie haben weit über 30 Spiele gespielt, hat der Undurchsichtige die Kneipe inzwischen verlassen. Sie stehen buchstäblich mit leeren Händen da, Sie haben fast alles verloren und können gerade noch die Rechnung begleichen. Auf dem Weg nach Hause beschließen Sie, der Sache noch einmal auf den Grund zu gehen. Was war passiert?
Nun, es ist offensichtlich, dass dies kaum ein Zufall sein kann – theoretisch zwar möglich –, aber Ihnen ist klar, dass der Undurchsichtige irgendeinen Vorteil gehabt haben muss. Darüber hinaus hatten Sie den Eindruck, dass Ihr Gegenüber, nach dem Sie Ihre Kombination geäußert haben, kurz nachdachte und dann die seine mitteilte. Wäre es möglich, dass er seine Kombination auf Ihre abgestimmt hat, obwohl doch alle gleichwahrscheinlich sind?
In der Tat wäre die Wahrscheinlichkeit für Gewinn oder Verlust gleich, wenn man die Münze nur 1 x werfen würde, also vorher auf Kopf oder Zahl setzt. Wird jedoch 3 x geworfen und muss man vorher eine Kombination benennen, die zum Gewinn führen soll, sieht die Sache etwas anders aus. Ihr Gegner hat sich das statistische Prinzip der Intransitivität zu Nutze gemacht und dementsprechend seine Taktik ausgelegt. Diese besagt, dass eine bestimmte Kombination anderen Kombinationen unterlegen und gleichzeitig überlegen sein kann. Welche Kombinationen unterlegen bzw. überlegen sind, hängt von der Wahl der ersten Kombination ab, die ja immer Sie getroffen haben. Der vermeintliche Vorteil, beginnen zu dürfen, war also in Wirklichkeit ein schwerwiegender Nachteil. Betrachten wir dazu ein kurzes Beispiel:
Nehmen wir an, Sie hätten die Kombination Z-Z-Z gewählt, so würden Sie dann gewinnen, wenn Zahl genau 3 x hintereinander geworfen wird. Ihr Gegner hat sich auf Ihre Wahl hin für K-Z-Z entschieden – warum? Nach wie vor ist a priori, also bevor die Serie der Würfe beginnt, das Auftreten für beide Kombinationen gleichwahrscheinlich. Die Wahrscheinlichkeit, dass seine Kombination vor der Ihren geworfen wird, ist allerdings höher. Nehmen wir an, es fällt Z-Z-K-Z-K, bisher hat noch niemand gewonnen, keine der beiden Kombinationen ist eingetreten, es geht also weiter. Nach wie vor brauchen Sie 3 x Zahl hintereinander zum Gewinnen, er hingegen braucht nur 2 x Zahl hintereinander und gewinnt, bevor 3 x Zahl für Ihren Gewinn überhaupt auftreten kann, hat er schon gewonnen. Er ist Ihnen also bildlich gesprochen immer einen Schritt voraus. Sehen wir uns dieses konkrete Beispiel zum besseren Verständnis nochmals in der folgenden Grafik an:
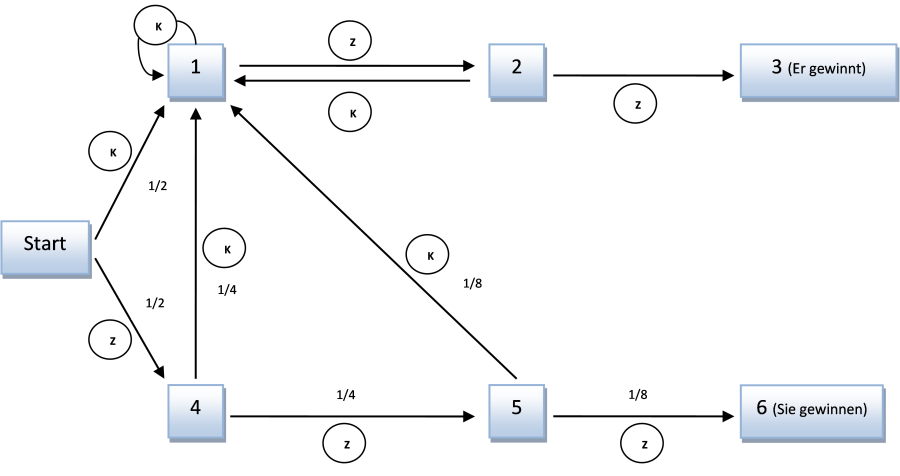
Abbildung 1: Schematische Darstellung des Spielverlaufs und deren Wahrscheinlichkeiten
Gehen wir das Ganze nun Schritt für Schritt durch. Wenn im ersten Wurf Zahl geworfen wird, befindet sich die Serie im Knoten (=Zustand) 4, die Pfeile stellen die entsprechenden Würfe (=Ereignisse) dar. Fällt nun beim nächsten Wurf wieder Zahl, sind Sie kurz vorm Ziel bei Knoten 5. Im dritten Wurf fällt nun aber Kopf, wir befinden uns nun im Knoten 1. Die traurige Nachricht: Egal was ab jetzt passiert, Sie können nur noch verlieren, denn es gibt kein Zurück mehr auf die Siegerstraße. Sollte danach wieder Kopf fallen, so verbleibt die Serie im Knoten 1 – nichts ändert sich. Fällt danach irgendwann wieder Zahl, so gelangt man zu Knoten 2 und Ihr Gegner steht nun seinerseits kurz vorm Ziel, da bereits K-Z geworfen wurde und er auf K-Z-Z gesetzt hat. Sollte nun wieder Kopf fallen, geht es zurück zu Knoten 1 und wir bleiben bei Knoten 1, bis irgendwann wieder Zahl geworfen wird und wir wieder bei Knoten 2 stehen. Sollte dann ein zweites Mal Zahl fallen, so hat unser Gegner schon gewonnen (K-Z-Z). Die Kombination Z-Z-Z kann nicht mehr erreicht werden.
Zusammengefasst: Wenn nur ein einziges Mal Kopf in der laufenden Serie geworfen wird, ist es für Sie nicht mehr möglich zu gewinnen, da bevor 3 x Zahl (für Ihren Gewinn) geworfen werden kann, zwingend 2 x Zahl geworfen werden muss und der Gegner gewinnt. Wie stehen nun die Chancen, bei diesem Beispiel tatsächlich mit der Kombination Z-Z-Z zu gewinnen? Verfolgen wir den Pfad über die Knoten 4, 5 und 6 bis zu Ihrem Gewinn ergibt sich die Wahrscheinlichkeit von 1/8. Alle anderen Pfade, die zwangsläufig früher oder später über Knoten 1 laufen müssen, ergeben die Wahrscheinlichkeit 1/2+1/4+1/8=7/8. Ihr Gegner hat also einen immensen Vorteil in dieser Konstellation – seine Wahrscheinlichkeit zu gewinnen ist 7 x höher als Ihre, die Sie ursprünglich als fifty-fifty Chance eingestuft hatten.
Man kann zeigen, dass es für alle Kombinationen möglich ist, eine überlegene Kombination zu finden, welche eine höhere Gewinnwahrscheinlichkeit aufweist. Gleichwohl kann diese überlegene Kombination gegenüber einer anderen wiederum unterlegen sein, das gesamte Spiel ist intransitiv. Wählen Sie im folgenden Spiel K-Z-Z als Kombination (die Ihr Gegner gerade erfolgreich genutzt hat), so wird Ihr Gegner diesmal K-K-Z wählen, er ist nun nicht mehr ganz so hoher Favorit wie im ersten Spiel, hat aber statistisch dennoch eine 2/3 Chance, auch diese Partie für sich zu entscheiden und gewinnt bei dieser Konstellation im Mittel doppelt so oft wie Sie. Treten Sie mit K-K-Z gegen ihn an, so wird er Z-K-K wählen und ist nun sogar wieder in 3/4 der Fälle ein Gewinner. Da seine Gewinnchance nie unter den Wert von 2/3 fällt, kann er Ihnen großzügig anbieten, 15 Euro auszuzahlen, wenn Sie gewinnen und er nur 10 Euro von Ihnen kassiert, wenn er gewinnt. Selbst bei einer Gewinnwahrscheinlichkeit von „nur“ 2/3 bleibt sein Erwartungswert immer noch positiv.
Ein interessanter, ungewöhnlich teurer, aber dafür äußerst aufschlussreicher Abend neigt sich nun dem Ende zu, als Sie bereits auf dem Weg nach Hause sind. Immer noch sind Sie in Gedanken und grübeln, was es nun mit diesem Spiel auf sich haben mag. Kurz vor Ihrem Haus angekommen, suchen Sie in Ihrer Manteltasche nach dem Haustürschlüssel und finden zu Ihrer Überraschung einen kleinen Brief, den Ihnen der Undurchsichtige unbemerkt in die Tasche gesteckt haben muss:
„Lieber Freund, nachdem Sie nun den einen oder anderen Taler verloren haben, möchte ich Ihnen als kleinen Trost das Geheimnis des Spiels verraten:
Nehmen Sie die Kombination Ihres Gegners, setzen Sie die ersten beiden Stellen an Ihre letzten beiden Stellen und wählen Sie an erster Stelle das Gegenteil der zweiten Stelle Ihres Gegners.“
Erstaunt lesen Sie den schon eingerissenen und etwas ramponierten Brief ein zweites und ein drittes Mal.
Sollte den Undurchsichtigen zuvor etwa das gleiche Schicksal ereilt haben, wie Ihnen heute Abend?
