Darüber hinaus werden diese Verfahren in allen Statistik-Lehrbüchern besprochen und das Internet bietet zudem zahlreiche Quellen, sich mit diesen Techniken anzufreunden und das eigene Datenmaterial auf diesem Wege auszuwerten. Zu häufig werden diese Methoden jedoch eingesetzt, ohne die recht strengen Modellprämissen, v.a. bei Messwiederholungsdesigns und Paneldaten, zu überprüfen. Nur die Einhaltung dieser Bedingungen garantiert uns jedoch gültige und unverzerrte Ergebnisse. Um welche Voraussetzungen es unter anderem geht, wollen wir im Folgenden veranschaulichen.
Ein Beispiel aus der empirischen Praxis
Nehmen wir an, wir sind an einem neuen Mittel zur Blutdrucksenkung interessiert und es wurde eine Stichprobe von Hypertonikern damit behandelt. Wir haben vor der ersten Verabreichung des Medikaments eine Prä-Messung durchgeführt und anschließend eine Post- sowie drei Follow-up-Messungen, um genaue Informationen über den Verlauf zu generieren. Die folgende Grafik zeigt einen Auszug unserer Datenmatrix, insgesamt konnten 26 Patienten rekrutiert werden, gemessen wurde der systolische Blutdruck in mmHg:
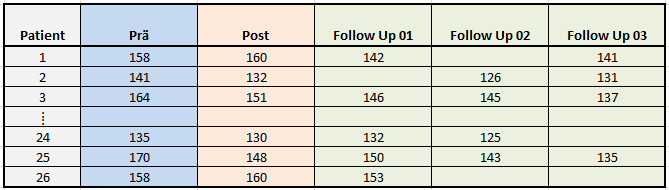
Tabelle 1: Auszug einer Datenmatrix mit wiederholten Messungen im wide-Format
Der Ausschnitt zeigt die Daten der ersten und letzten drei Patienten. Zunächst wird ersichtlich, dass der systolische Blutdruck zu fünf Zeitpunkten (Prä, Post, Follow Up 01, Follow Up 02, Follow Up 03) gemessen wurde, wobei offensichtlich unvollständige Daten vorliegen – in der Praxis eher die Regel als die Ausnahme, vor allem dann, wenn die Studie ambulant und nicht stationär durchgeführt wurde. In unserem Beispiel liegen nur von Patient 3 und Patient 25 vollständige Daten vor, bei den anderen Patienten fehlt entweder eine oder es fehlen sogar mehrere Messungen.
Welche Fragen wollen wir beantworten?
Unsere Hypothesen zielen darauf ab, Unterschiede zwischen den Zeitpunkten bezüglich unserer abhängigen Variable (dem systolischen Blutdruck) nachzuweisen. Noch konkreter erwarten wir durch die Gabe des Medikaments, dass der Blutdruck von Prä nach Post fällt und dann bei den Follow-up-Messungen dieses Niveau gehalten wird bzw. stagniert. Kämen wir auf die Idee, eine klassische Varianzanalyse ohne Messwiederholung durchführen und die einzelnen Zeitpunkte als Gruppen zu definieren, würden wir die Abhängigkeit der Messungen zwischen den Zeitpunkten ignorieren und erhielten verzerrte Ergebnisse.
Wie aus den Daten zu erkennen ist, hängen die Messungen eines Patienten über die Zeit natürlich voneinander ab. Setzen wir daher eine Varianzanalyse mit Messwiederholung ein, tragen wir dieser Abhängigkeit Rechnung. Leider verlangt diese Analysetechnik noch ein wenig mehr von unseren Daten und stellt uns ein weiteres Mal auf die Probe. Um valide Ergebnisse zu erhalten – was natürlich immer das Ziel wissenschaftlich fundierter Forschung sein sollte – müssen zudem noch vollständige Daten vorhanden sein. Sind die Daten unvollständig, so kann der entsprechende Fall – in unserem Beispiel der Patient – nicht berücksichtigt werden. Liegen uns wie bei Patient 2 also vier Messungen vor und nur eine Messung fehlt (hier Follow Up 01), wird der Patient nicht berücksichtigt. Er wird also komplett aus der Analyse ausgeschlossen, was für uns mehr als ärgerlich ist, sind wir doch dankbar für jeden Probanden, den wir rekrutieren konnten. Von unseren sechs Patienten, deren Auszug uns in der Tabelle vorliegt, könnten wir also nur Patient 3 und Patient 25 berücksichtigen und würden damit auf einen Großteil unserer Informationen verzichten. Dieses „Ausschlussverfahren“ wird in den statistischen Softwarepaketen auch als listenweiser Fallausschluss bezeichnet. In unserem Beispiel stellt der Ausschluss von Patienten, die nicht zu allen Zeitpunkten gemessen wurden, jedoch ein inakzeptables Vorgehen dar.
Darüber hinaus müssen wir uns noch mit einer weiteren Hürde beschäftigen, die uns das Leben schwer macht: Der sogenannten Sphärizitätsannahme. Diese besagt nämlich, dass die Varianzen der Differenzen zwischen den Zeitpunkten homogen sein sollten. Ist die Annahme stark verletzt, werden wir auch hier nicht so recht glücklich und sollten uns nach Alternativen umsehen, im Besonderen natürlich, wenn wir es mit unvollständigen Daten und verletzter Sphärizität zu tun haben.
Die Lösung
Gibt es nun aber eine Methode, die uns die Heilung unserer statistischen Probleme verschafft und uns zu verlässlichen Ergebnissen führt? Die Antwort lautet ja, allerdings müssen wir dafür den Preis erhöhter Schwierigkeit und Komplexität bezahlen. Gemeint sind Multilevel bzw. Mixed Models, im Deutschen auch als Mehrebenenmodelle bezeichnet. Es existieren noch eine Fülle weiterer Synonyme in der Literatur, die aber das gleiche meinen. Dazu zählen die linearen gemischten Modelle, hierarchische Modelle sowie Modelle mit festen und zufälligen Effekten. Mixed oder gemischt bezieht sich immer auf das Vorhandensein von festen und zufälligen Effekten, es werden aber die gleichen statistischen Prozeduren – wie zum Beispiel bei longitudinalen Daten auch ohne zufällige Effekte – eingesetzt, wie bei klassischen Mixed Models.
Inzwischen sind diese Modelle in allen gängigen Softwarepaketen enthalten, in IBM SPSS Statistics heißt die Prozedur „MIXED“, in SAS wird sie „proc mixed“ genannt. Während die Umsetzung per Syntax in den Paketen relativ übersichtlich gestaltet ist, gilt für die Durchführung der Analysen über die Menüs leider das Gegenteil. Die Flexibilität der Modellierung, die dem Anwender zur Verfügung steht, kann schnell zur Verwirrung führen – das betrifft vor allem SPSS.
Worin bestehen aber nun die Vorteile dieser Modelle?
Zum einen können sie problemlos mit fehlenden Daten umgehen und nutzen somit – im Gegensatz zur RM ANOVA mit Missings – alle Informationen des Datensatzes aus. Voraussetzung dafür ist jedoch, dass der Datensatz im vertikalen oder sogenannten Long-Format vorliegt. Das bedeutet, dass die fünf Zeitpunkte in unserem Beispiel nicht in fünf Spalten, sondern in fünf Zeilen organisiert sind. Fehlt nun eine Messung, ist also ein Wert in einer Zeile leer, werden dennoch alle anderen Messungen des Patienten mitberücksichtigt. Dies entspricht im statistischen Sinne einem univariaten und nicht mehr dem multivariaten Ansatz. Pro Patient liegen in unserem Beispiel fünf Zeilen vor, der Blutdruck als Zielgröße oder abhängige Variable ist in nur einer Spalte organisiert, wie die folgende Grafik für die ersten beiden Patienten unserer Stichprobe verdeutlicht:
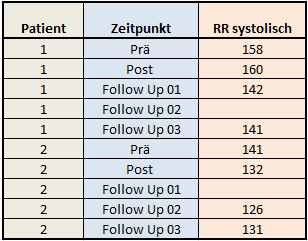
Tabelle 2: Auszug einer Datenmatrix mit wiederholten Messungen im long-Format
Eine Umstrukturierung der Daten vor den Analysen ist also vonnöten. Es wird nun auch ersichtlich, warum man von einem Mehrebenenmodell oder Multilevel Model spricht: Die erste Ebene bildet der Zeitpunkt, die zweite Ebene der Patient. In diesem Beispiel haben wir es mit zwei Ebenen, also dem einfachsten Fall, zu tun. Dabei sind die Messungen der ersten Ebene (Zeitpunkt) unter der zweiten Ebene (Patient) verschachtelt. Die wiederholten Messungen eines Patienten sind voneinander abhängig und korrelieren miteinander. Longitudinale Daten sind also ein spezieller Fall oder Teil eines Mehrebenenmodells. So wäre darüber hinaus eine dritte Ebene denkbar, z.B. die Klinik. Würden wir in einer multizentrischen Studie mehrere Kliniken in unserem Design berücksichtigen, so wäre dann davon auszugehen, dass Patienten in ein und derselben Klinik ähnlichere Ergebnisse aufweisen, als zwischen verschiedenen Kliniken – beispielsweise aufgrund der gleichbleibenden Qualität der pflegerischen Betreuung innerhalb einer Klinik. Folgende Grafik zeigt ein Mehrebenenmodell mit drei Ebenen, wobei Ebene 1 den Messwiederholungen (=Zeitpunkt) entspricht:
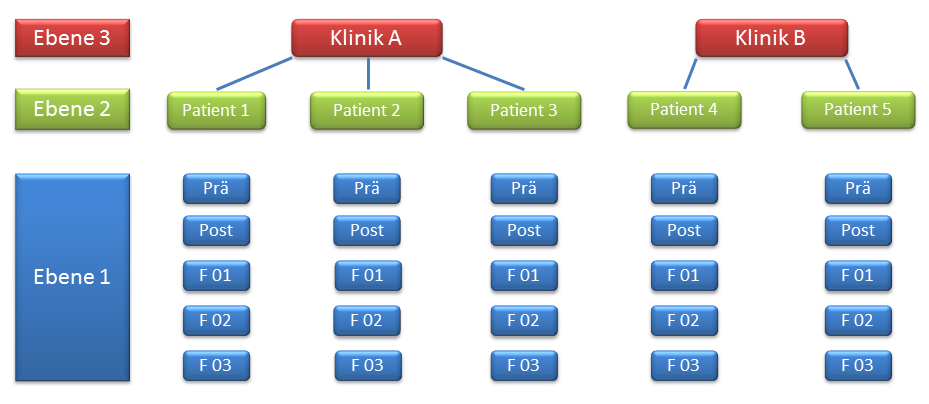
Abbildung 1: Schematische Darstellung eines Mehrebenenmodells
Die wiederholten Messungen (Ebene 1) sind unter den Patienten geschachtelt (oder geclustert), die Patienten (Ebene 2) wiederum unter den Kliniken (Ebene 3).
Hohe Flexibilität in der statistischen Modellierung
Nachdem wir wissen, dass fehlende Werte oder Drop-outs kein Problem im Rahmen von Multilevel Models darstellen, drängt sich die Frage nach einer weiteren Bedingung der klassischen Modelle auf: Der Sphärizität. Auch hier gibt es gute Nachrichten, da wir nun die Möglichkeit haben, die Varianz-Kovarianz-Struktur unserer wiederholten Effekte beliebig zu modellieren. Wir könnten beispielsweise über die Varianz-Kovarianz-Struktur überhaupt keine Annahmen machen und somit davon ausgehen, dass die Varianz des systolischen Blutdrucks zu jedem Zeitpunkt unterschiedlich ist und auch die Kovarianz zweier beliebiger Zeitpunkte schwanken darf. Dieses Muster wird als „unstrukturiert“ bezeichnet, erfordert jedoch ein Maximum an Parametern, die geschätzt werden müssen. Gehen wir aber davon aus, dass die Varianzen zu allen Zeitpunkten annähernd gleich sind und die Kovarianz mit zunehmendem zeitlichem Abstand geringer wird, so könnten wir explizit auch diese Struktur vorgeben, die man als „autoregressiv“ bezeichnet. Sie benötigt im Vergleich zur unstrukturierten Matrix weniger Parameter, das Modell wird einfacher. Im Gegensatz zum Allgemeinen Linearen Modell ist die Voraussetzung der Sphärizität nun keineswegs mehr zwingend, es sei denn, es wird der multivariate Ansatz einer Varianzanalyse mit Messwiederholung gewählt, der jedoch andere Probleme mit sich bringt.
Fazit und Ausblick
Warum sind Mehrebenenmodelle aber deutlich komplexer und werden seltener eingesetzt? Zum einen fällt es vielen Anwendern schwer, im Rahmen von gemischten Modellen zwischen festen und zufälligen Effekten zu unterscheiden bzw. diese korrekt zu bestimmen und in das Modell mit aufzunehmen. Die Schätzung der Parameter erfolgt im Gegensatz zu „rechnerischen Verfahren“ bei linearer Regression oder Varianzanalyse durch iterative Verfahren mittels Maximum-Likelihood-Methode.
Des Weiteren erfordert auch das flexible Instrument der Festlegung der Varianz-Kovarianz-Struktur einige Erfahrung und ist anspruchsvoller, als einfach nur Sphärizität vorauszusetzen oder aber bei Verletzung dieser, p-Werte durch die Korrektur der Freiheitsgrade zu adjustieren. Gleiches gilt für die Interpretation und die Signifikanztests der ermittelten Parameter. Kommen auch noch weitere zufällige Effekte hinzu, wird die statistische Modellierung noch umfangreicher und setzt entsprechendes methodisches Know-how und vor allem Erfahrung im Umgang mit der statistischen Software voraus. Gleichwohl zeigt sich in der empirischen Praxis, dass zu häufig Methoden wie z. B. die Varianzanalyse eingesetzt werden, ohne die Voraussetzungen und den möglichen Datenverlust eingehend zu prüfen. Auch wenn die Verfahren des Allgemeinen Linearen Modells relativ robust gegenüber Verletzungen reagieren, sollte man sie nicht blind anwenden, sondern ihren Einsatz kritisch hinterfragen.
Cluster- und longitudinale Daten kommen vor allem in den Sozialwissenschaften und der Medizin recht häufig vor, sei es im Rahmen einer kleinen Studie für eine medizinische Doktorarbeit oder aber eine groß angelegte klinische Studie zur Einführung eines neuen Wirkstoffs.
Mehrebenenmodelle bieten Ihnen die Möglichkeit, Effekte verlässlich zu schätzen und auf statistische Signifikanz zu prüfen. Sie sollten diesen im Zweifel also immer den Vorzug geben, um valide und aussagekräftige Ergebnisse zu erhalten, auch wenn der Weg zu diesen Ergebnissen oftmals deutlich schwieriger und anspruchsvoller ist.
