Beispiel für eine gerichtete Hypothese
Wir vermuten beispielsweise, dass Einkommen und Bildung positiv miteinander korrelieren und formulieren unsere Hypothese dementsprechend. Würden wir nur behaupten, es besteht irgendein Zusammenhang zwischen den beiden Merkmalen, geben die Richtung aber nicht vor, so haben wir es mit einer ungerichteten Fragestellung zu tun.
Ein Vorteil: Höhere statistische Power
Gerichtete Hypothesen, so sie denn sachlogisch richtig und theoretisch gut fundiert sind, haben den Vorteil einer höheren Teststärke (Power) und werden mit einem einseitigen Signifikanztest überprüft. Im Gegensatz dazu werden Hypothesen, die ungerichtet aufgestellt wurden, immer zweiseitig getestet. Vom methodischen Standpunkt aus ist man mit einer ungerichteten Fragestellung immer auf der sicheren Seite, sollte sich aber nicht scheuen, auch gerichtete Hypothesen aufzustellen, da man dann einseitig testen darf und in den Genuss einer höheren statistischen Power kommt.
Die richtigen Begrifflichkeiten sind entscheidend
Woher kommt nun aber die Verwirrung, die im Zusammenhang mit dem Signifikanztest steht? Der Grund dafür liegt vor allem in der weitverbreiteten Meinung, dass nur die Signifikanztests einseitig testen können, deren entsprechende Prüfgröße symmetrisch verteilt ist, wie z. B. beim T-Test (T-Verteilung) oder z-Test (Normalverteilung). Andere Verteilungen, wie die Chi-Quadrat- oder F-Verteilung, die nur positive Werte aufweisen, sind nicht symmetrisch, wenn wir uns die zugehörigen Dichtefunktionen anschauen:
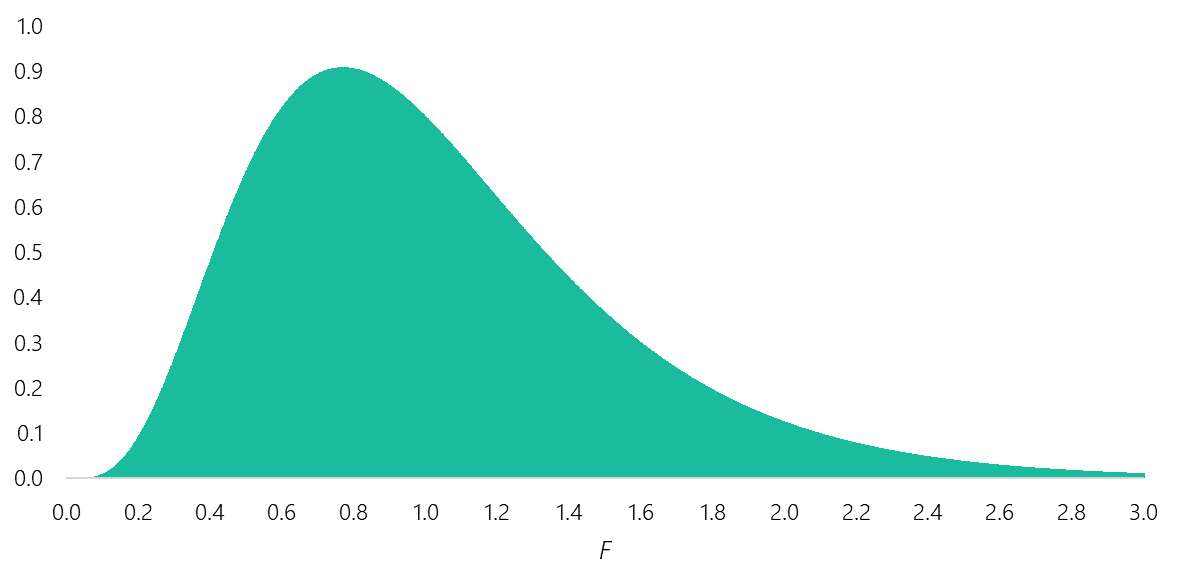
Abbildung 1: F-Verteilung mit df Zähler = 10 und df Nenner = 50
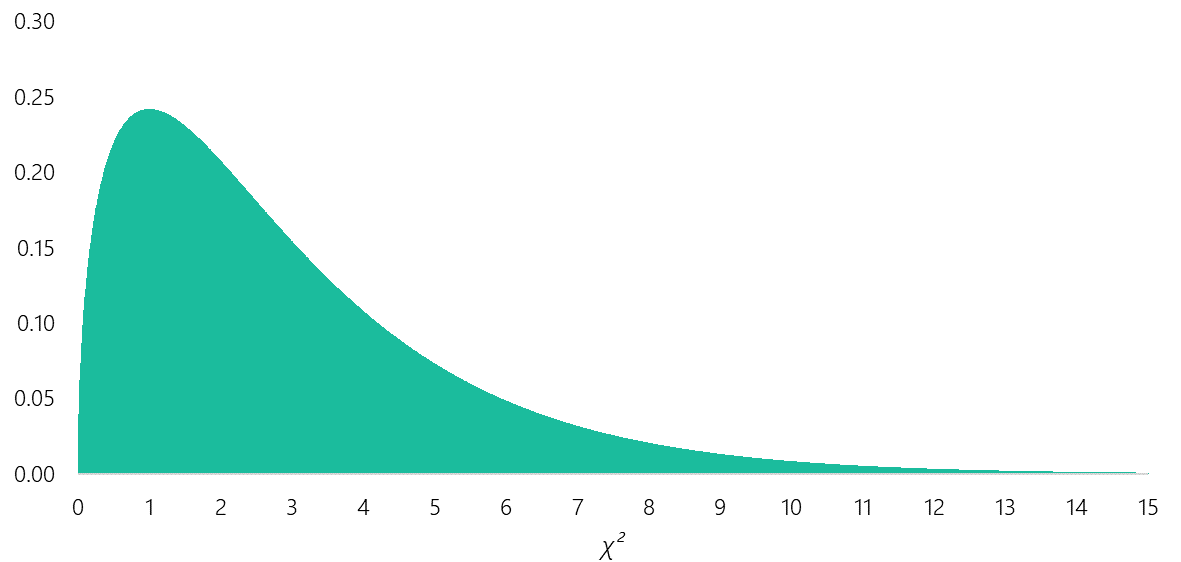
Abbildung 2: Chi-Quadrat-Verteilung mit df = 3
Das eine hat allerdings mit dem anderen nichts zu tun, da der einseitige bzw. zweiseitige Test und die Symmetrie der Prüfverteilung zwei unterschiedliche Konzepte sind. Im Englischen fällt diese inhaltliche Unterscheidung leichter, da man hier von one- or two-sided bzw. von one- or two-tailed spricht. Es ist daher sinnvoll, diese Terminologie auch im Deutschen zu verwenden, um etwas mehr Klarheit in die Thematik zu bringen. Symmetrische Prüfgrößen können immer one- oder two-tailed geprüft werden, nicht symmetrische immer nur one-tailed (am rechten Ende der Verteilung).
Generell gilt, dass Chi-Quadrat- oder F-Test immer zweiseitige Fragestellungen testen, obwohl sie nur one-tailed prüfen können. Bei symmetrischen Verteilungen und deren Tests wie T– oder z-Test, korrespondiert hingegen der einseitige Test direkt mit der one-tailed Prüfung und der zweiseitige Test mit der two-tailed Prüfung. Möchten wir einen einseitigen Test durchführen und benötigen einen Chi-Quadrat-Test, so ist das α-Niveau zu verdoppeln oder der empirisch ermittelte p-Wert zu halbieren, um die gerichtete Hypothese auf statistische Signifikanz zu prüfen.
Ein Beispiel zum besseren Verständnis
Lassen Sie uns gemeinsam ein Beispiel betrachten: Bei der Unterschiedsprüfung zwischen 2 Gruppen (A und B) möge das Ergebnis eines T-Tests für unabhängige Stichproben einen Wert von p = .042 ergeben haben und wäre somit statistisch signifikant (da p < .05). Da die Hypothese ungerichtet formuliert wurde, also nur behauptet wurde, dass überhaupt ein Unterschied besteht, ohne eine Richtung vorzugeben, haben wir es mit dem Ergebnis eines zweiseitigen Tests zu tun. Berechnen wir nun eine einfaktorielle Varianzanalyse mit denselben Daten, erhalten wir einen F-Wert und die entsprechende Signifikanz, die exakt die gleiche ist, nämlich p = .042. Beide Verfahren kommen zum gleichen Ergebnis, obwohl unterschiedliche Prüfgrößen eingesetzt werden. Das Ergebnis des F-Tests der Varianzanalyse entspricht also dem Ergebnis eines zweiseitigen T-Tests, obwohl die Signifikanz beim F-Test one-tailed geprüft wurde!
Nehmen wir nun an, wir hätten unsere Hypothese gerichtet formuliert und behauptet, dass Gruppe A höhere Werte aufweist als Gruppe B, so sollten und müssten wir einseitig testen. Viele Statistikprogramme geben nur den p-Wert des zweiseitigen Tests aus. Für den einseitigen Test müssen wir den empirischen p-Wert selbst halbieren. Für den einseitigen Test ergibt sich in unserem Beispiel somit ein p-Wert von .042/2 = .021, wir haben es wieder mit einem statistisch signifikanten Ergebnis zu tun. Das gleiche Konzept könnten wir auch auf den F-Test anwenden und würden zum gleichen Ergebnis kommen.
Die folgenden Diagramme verdeutlichen den Ablehnungsbereich der Nullhypothese bei konstantem Signifikanzniveau (α = .05) für den zwei- und einseitigen F-Test mit df (Zähler) = 10 und df (Nenner) = 50. Der Ablehnungsbereich der Nullhypothese (orange markierte Fläche) ist beim einseitigen Test doppelt so groß im Vergleich zum zweiseitigen Test.
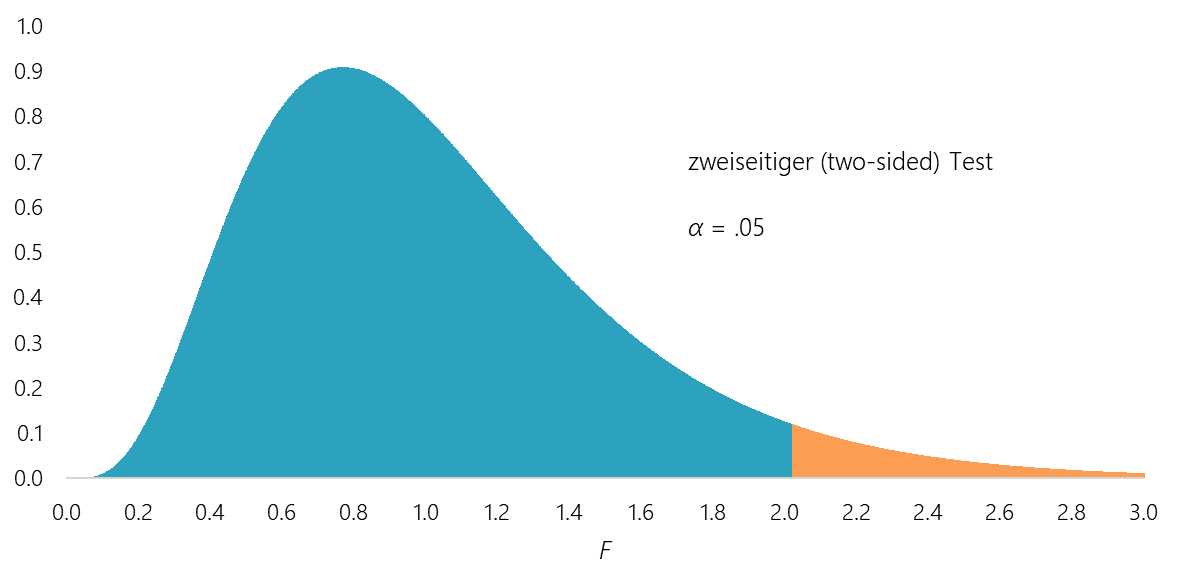
Abbildung 3: Zweiseitiger Signifikanztest
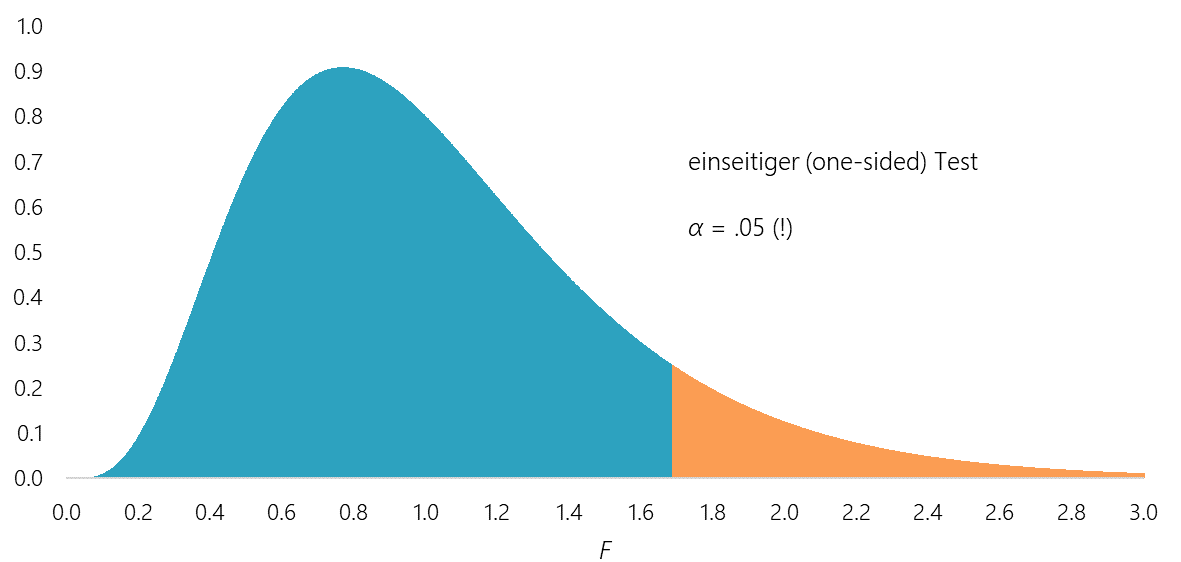
Abbildung 4: Einseitiger Signifikanztest
Ein weiteres Beispiel mit Häufigkeiten
Als zweites Beispiel möge eine 2 x 2 Kreuztabelle (4-Felder-Tafel) dienen, bei der die Häufigkeiten zweier nominaler Merkmale abgetragen werden. Der Chi-Quadrat-Test prüft nun die Unabhängigkeit der beiden Merkmale zweiseitig, obwohl wir es mit einer Prüfverteilung zu tun haben, bei der die Signifikanz nur one-tailed berechnet wird. Die zweiseitige Signifikanz des Chi-Quadrat-Tests korrespondiert auch mit der zweiseitigen Signifikanz der Korrelation der beiden Merkmale. Gehen wir aber davon aus, dass beispielsweise ein negativer Zusammenhang zwischen den Merkmalen besteht und somit die Hypothese gerichtet formuliert wurde, müssen wir einseitig testen. Berechnen wir den p-Wert für die einseitige Korrelation, so entspricht sie wieder dem halbierten p-Wert des zweiseitigen Tests. Wollen wir also das Ergebnis eines einseitigen Chi-Quadrat-Tests interpretieren, müssen wir auch hier den empirisch ermittelten p-Wert des zweiseitigen Tests halbieren.
Es sei angemerkt, dass der einseitige Chi-Quadrat- und F-Test nur sinnvoll eingesetzt werden kann, wenn die Verteilung einen Freiheitsgrad aufweist (beim F-Test einen Zählerfreiheitsgrad), da ansonsten keine eindeutige Richtung mehr vorgegeben werden kann.
Fazit
Zusammenfassend ist festzuhalten, dass der ein- oder zweiseitige Test unabhängig davon ist, welche Prüfgröße bzw. Prüfverteilung eingesetzt wird. Die Berechnung des empirischen p-Wertes auf Grundlage der Daten kann one-tailed oder two-tailed erfolgen, einen direkten Zusammenhang zwischen einseitig und one-tailed bzw. zweiseitig und two-tailed besteht nur bei symmetrischen Prüfverteilungen.
